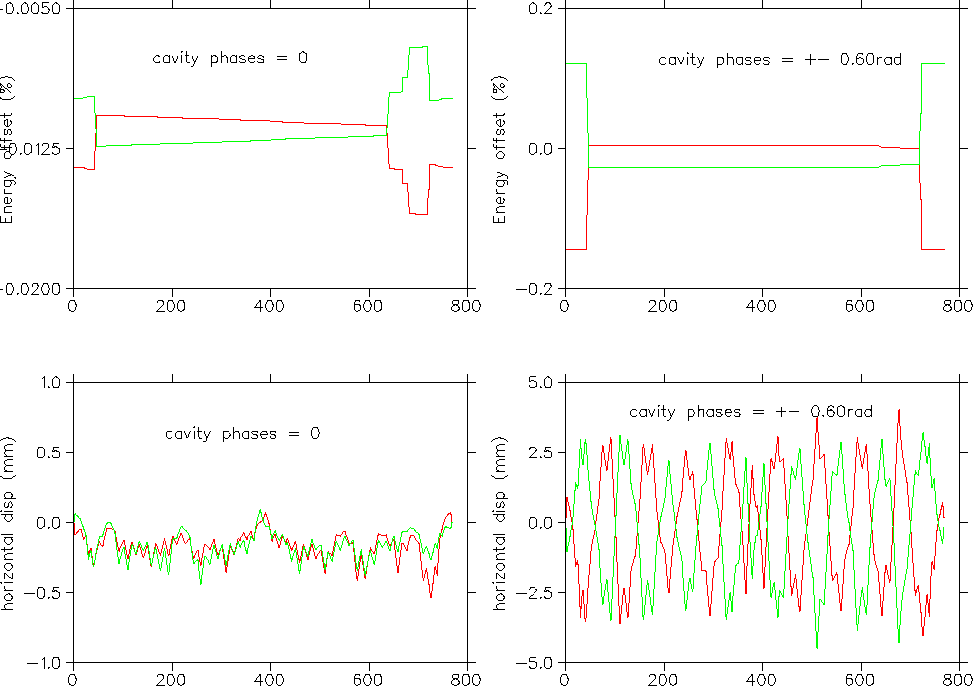
If Q_ext = 1e6, R/Q=89ohms, V_acc=2.5MV, and I=50mA the
- P_{pass} = 70.2kW
- E = 1.4MV
- phi = 0.6 radians
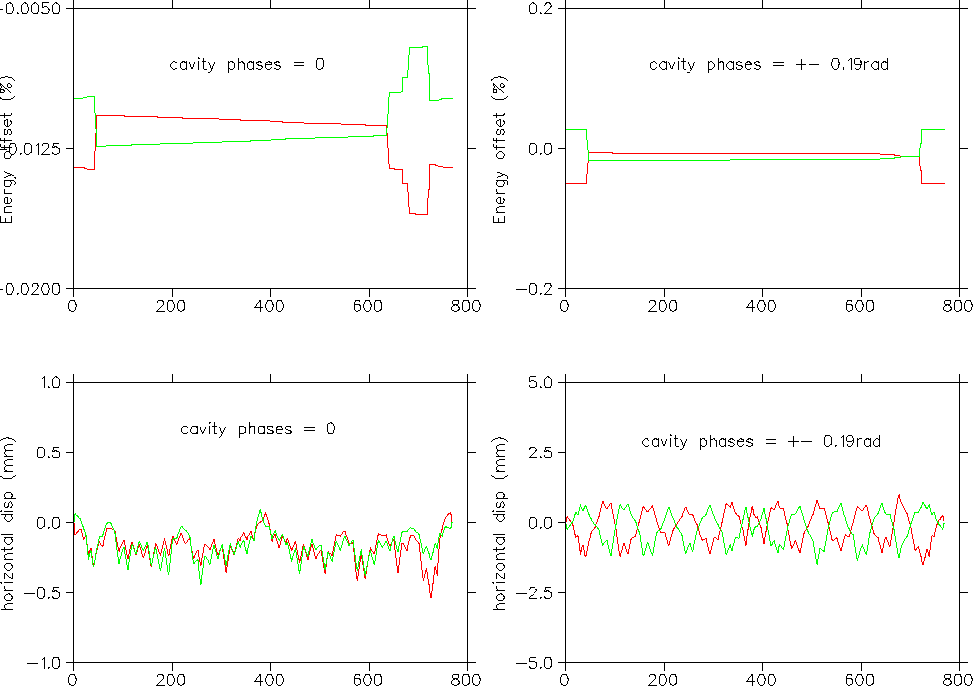
Consider the effect of adding 1.4MV at the west cavities and then subtracting 1.4MV in the east. Note that the energy loss due to synchrotron radiation is negligible in comparison to energy shifts from the RF. The results are shown in the plot. The pair on the left show the closed orbits with phi=0, that is no energy gain at either cavity. The pair on the right show closed orbits with phi=0.6radians for the west cavities and phi=-0.6radians for the east. The upper pair show energy vs s and the lower pair horizontal displacement vs s. Separators are off. Red is positrons and green is electrons.
- P_{pass} = 23.4kW
- E = 0.468MV
- phi = 0.19 radians