Symmetric diblock copolymers - degree of polymerization

Detlef Smilgies, CHESS

The phase behavior and the microstructure of block copolymers depends on the volume
taken up by each block. Hence a symmetric diblock copolymer consists of two coupled
chains filling the same volume. Since the monomers usually differ in size, this means that
the number of monomers within each of the blocks differs. As an example we will study
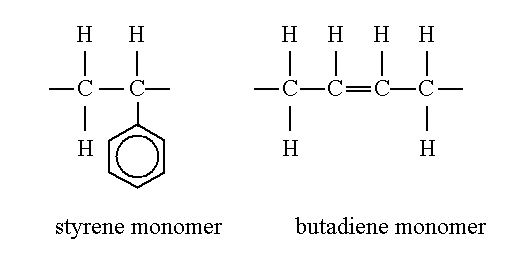
polystyrene-polybutadiene (PS-PB).

Molar Volume of the Monomers

The styrene and butadiene monomers

monomers

contain 8 H and 8 C atoms and 4 C and 6 H atoms, respectively. Molar masses of the monomers
are

MS = 104.1 g
MB = 54.1 g

With the help of the densities of the homopolymers

ρPS = 1.05 g/cm3
ρPB = 0.89 g/cm3

we can calculate the molar volume of the S and B monomers:

vS = MS / ρPS vS = 99.2 cm3
vB = MB / ρPB vB = 60.8 cm3

Molar Volumes of the Blocks

If the block volume is given by Vblock, for a symmetric copolymer the chainlengths NS, NB for the two blocks
are given by:

NS vS = Vblock = NB vB

From this relation we obtain the ratio of the S and B chainlength

xSB = NS/NB = vB/vS xSB = 0.613 (1)

i.e. there is an excess of 40% B monomers necessary, so that the S- and B-blocks take up the same volume!

Finally, the total molar mass of PS-PB is given by:

M = NS MS + NB MB (2)

Even if there are no more detailed numbers given, we still have enough information now to determine the detailed
chemical composition of the block copolymer. Combining (1) and (2) yields

NB = M / (xSB MS + MB)
NS = xSB NB

Degree of Polymerization

There are several ways to define the degree of polymerization for a block copolymer. The most naive one is just
the total number of monomers:

N1 = NS + NB

A more sophisticated way is to use the geometric mean of NS and NB:

N2 = 2 sqrt{NS NB}

This corresponds to introducing a mean molar volume

v = sqrt{vS vB}

and N2 can be rewritten as

N2 = {NS vS + NB vB} / v = {NS sqrt(vS/vB) + NB sqrt(vB/vS)} = {NS sqrt(ρB/ρS) + NB sqrt(ρS/ρB)}

This way we can replace the unequal volumina and chain lengths by an effective completely symmetric copolymer
with N2 monomers of volume v with N2/2 monomers of each kind. Obviously, this "effective" copolymer is much
easier to implement in a Monte-Carlo simulation than the actual one.

Ref: Wiesner and coworkers, Macromolecules 34, 2001 on P(I-b-EO) bcps.

If a whole series of block copolymers containing always one of the blocks is to be compared, the degree of polymeriztion can be defined with respect to the common block (here B):

N3 = {NS vS + NB vB} / vB

A comparison of all values as well as the values obtained in [Papadakis] are shown below for a series of PS-PB
symmetric diblock copolymers.

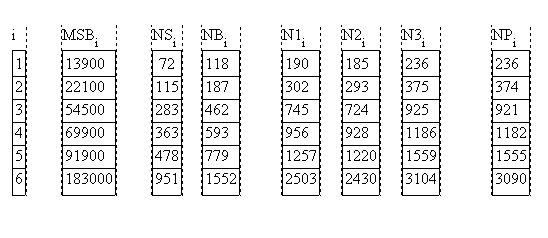
Table 1

ref Papadakis et al., Europhys. Lett.