If we introduce a new surface unit cell or a superstructure unit cell, we would like to know how the new atomic coordinates (x,y,z), the new reciprocal lattice vectors (a*,b*,c*), and the new indices (hkl) relate to the original ones. If the matrix S denotes the basis change:

^T(a’,b’,c’) = S ^T(a,b,c)

then we get for the atomic coordinates

r = (x,y,z) ^T(a,b,c) = (x,y,z) S^-1 S ^T(a,b,c) = (x’,y’,z’) ^T(a’,b’,c’)

with

(x’,y’,z’) = (x,y,z) S^-1

For compactness of notation, matrices of vectors are used, which follow the usual rules of matrix operations. ^T(…) denotes the transposed matrix.

The new reciprocal lattice vectors can be derived with the help of the dyadic product

2p 1  =  ^T(a,b,c) (a*,b*,c*)
         = S  ^T(a,b,c) (a*,b*,c*) S^-1
         = { S ^T(a,b,c)} {(a*,b*,c*) S^-1 }
         = ^T(a’,b’,c’) (a’*,b’*,c’*)

where 1 is the unit matrix, and hence

^T(a’*,b’*,c’*) = S*  ^T(a*,b*,c*)

with S* = ^TS^-1.

Here we made use of the interchangibility of transposition and inversion:

^T(S^-1) = (^TS)^-1 = ^TS^-1

and the transposition rule for matrix products

^T(A B) = ^TB ^TA.

Finally we would like to calculate the new indices, which will follow the scheme we applied for the atomic coordinates:

q = (h,k,l) ^T(a*,b*,c*) = (h,k,l) S*^-1 S*  ^T(a*,b*,c*) = (h’,k’,l’) ^T(a’*,b’*,c’*)

and

(h’,k’,l’) =  (h,k,l) S*^-1 = (h,k,l) ^TS

We see that we can make use of any combination of the inversion (…)^-1 and transposition ^T(…) operations on the matrix of the basis change S:
 
 
 

Furthermore we see that, if we define the basis change by left multiplication in either space (the usual way), the transformation of the coefficients is done by right multiplication with the inverse matrix.
 

Examples:

The first three examples deal with the surface unit cells for the fcc lattices:

(picture)
 

1) fcc(100) surface unit cell

From the picture we see that

a' = (a+b)/2
b' = (b-a)/2
c' = c

2) fcc(110) surface unit cell

a' = (a+b)/2
b' = c
c' = (b-a)/2

a' = (a+b)/2
b' = (a+c)/2
c' = a + b + c

The next example shows a superstructure unit cell:
 

4) a p(2x1) superstructure cell

a' = 2a
b' = b
c' = c

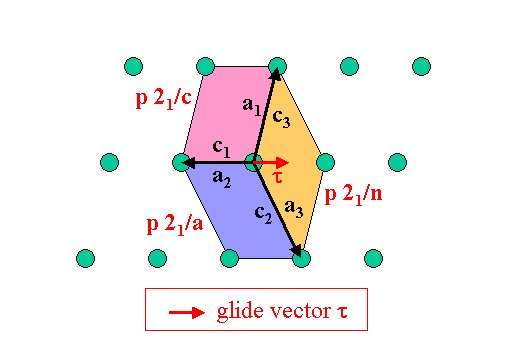
Finally we are going to study two application examples for the p 2₁/c space group (No.14) which is the most commonly observed space group for small organic molecules with over 200,000 known structures. First we note that for monoclinic structures, there are three possible choices of the unit cell in the a-c plane, if b is chosen as the special axis (i.e. the axis that is perpendicular to both a and c).

5) p2₁/a   to  p2₁/a

The molecules p-4p, p-5p, and p-7p have been described slightly differently than the well-studied molecule p-6p (para-sexiphenyl) yielding different Miller indices for the main reflections. However, the reason for this apparent difference between very similar molecules that differ only by the length of the phenyl chain, is a simple basis transformation.
By choosing

a' = -a
b' = -b
c' = a + c

6) p2₁/n   to   p2₁/c

The non-standard spacegroup p2₁/n can be transformed into the standard group p2₁/c by the same transformation as in example 5). As a check for a successful transformation, let's take a look at the index rule for the n glide plane:

for k=0: h+l=2n

(hkl) = (h'k'l') S

h=h'-l'
l=l'

for k'=0: l'=2n