The Scherrer Formula Revisited
Detlef-M. Smilgies, CHESS
The ubiquitous Scherrer formula [P. Scherrer, Göttinger Nachrichten
(1918)]
D = {K*lam} / {cos(th) dtth}
has been the workhorse of x-ray diffraction methods for
determining the average size of
scattering objects D from the width (fwhm) of the diffraction peak
Dtth, and aside from Bragg's law may be the most commonly referred to
formula in x-ray diffraction.
The original derivation has been refined in various other papers and
textbooks. Nowadays the
prefactor K is typically used between the bounds 0.9 < K <1.
Using the modern language of Fourier
transforms we provide an easy way to understand the shape of the Bragg
reflection and to derive a value for K.
Warren provides a straightforward, effective way to K: using the
scattering from a finite number of Bragg planes, K is determined from
the FWHM of the sin(Nx)/sin(x) function. In a more formal way,
that lends itself to further generalization, we shall rederive the result
in the language of Fourier transforms:
For small crystallites of micron size, i.e. smaller than the
dynamic extinction length, the kinematic approximation can be safely
applied. In this case the scattering intensity distribution is given
the squared modulus of the Fourier-transform of the electron density.
For an infinitely extended lattice this Fourier transform is an
infinite series of delta functions centered on the reciprocal lattice
with the prefactor for each reflection given by the structure factor of
the unit cell. In order to describe a finite crystal we follow
Patterson and introduce a shape function which is 1 inside its bounds,
and 0 elsewhere. The product of the shape function and the infinite
lattice yields a finite crystal of a shape given by the shape function.
Using the convolution theoreme, the intensity distribution of a
reflection of a finite crystal is then given by the convolution of the
delta functions at the reciprocal lattice points and the Fourier
transform of the shape function. Thus the shape function Fourier
transform defines the shape and width of the reflections.
A finite slab is cut out of an infinite number of Bragg planes by
multiplying the Bragg planes with a cut-off function
rect(z) = 1, z2 < R2; 0
The Fourier transform of rect(z) is the sin(x)/x function with x=qz.
The product in real space transforms to a convolution in reciprocal
space and the sharp Bragg peaks get smeared out in z-direction by
sin(x)/x. From this construction it is clear that this approach should
work well for lamellar systems.
Similarly we can define a circular and a spherical domain:
circ(x,y) = 1, x2+y2<R2; 0
sphere(x,y,z) = 1,x2+y2+z2<R2;0
The Fourier transforms of these cut-off functions are well-known in
small-angle scattering as the formfactor of a disk and of a sphere,
resp.
Circ(xi)= {2J1(xi)/xi}
...
Anisotropy
The scattering from an arbitrary ellipsoid can be obtained by realizing that any linear
transformation S (rotation, stretch, shear) applied to the shape will
be related to the distortion of the 1/2 value ellipsoid in q-space:
xi = qR = qT R = qT S-1 S R = (S-1T q)T (SR)
i.e. when the rela space distortion is given by S
The scattering intensities are then given by the modulus of the form
factors and are plotted in Fig 1. Note that the period of the
characteristic cut-off oscillations changes as a function of dimension,
where we note that the 3 cut-off functions introduced correspond to the
abstract spheres in 1,2, and 3 dimensions.
K-factor ....
spherical grains: K=1.15 most common case, usually K<=1 is used
anisotropic shapes in soft materials:
less anisotropic:
ellipsoid: sphere(: xi=sqrt(a2 x2 + b2 y2 + c2z2) : a,b,c=half axes
1)
oriented / crystalline: In anisotropic lattices often the particle
shape is anisotropic, too, as the growth or crystallization along
non-equivalent directions is different. For the characterization of
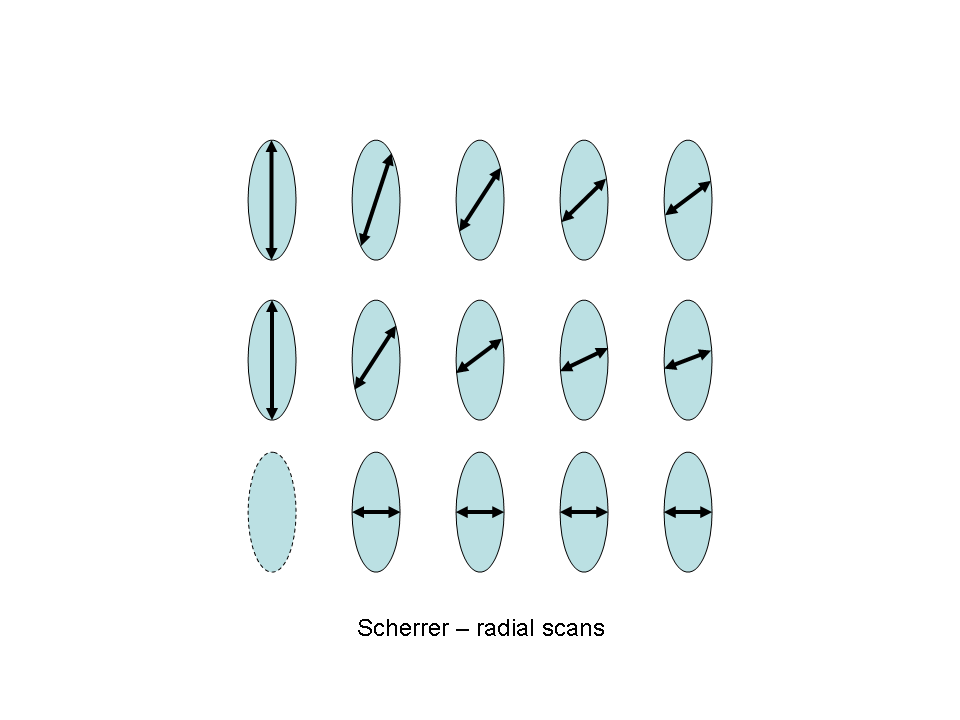
anisotropic shapes in crystalline materials, only radial scans should
be used for Scherrer analysis, since tangential scans are effected by
mosaicity and texture, and do not reflect pure shape information. As
soon as the powder reflections are indexed, the half-axes of the shape
ellipsoid can be determined from the low-index reflections. Care need
to be taken that the powder is not strained, as this will also effect
the peak widths. A good indication for strain is, if the peak width
changes in a series of reflections along the same radial vector, such
as (00L) or (HH0). If shape is the only determining factor, the FWHM of
such reflections should be identical. The width from a variety of
different radial directions can then be fitted to a shape ellipsoid
x2/a2 + y2/b2 + z2/c2 = 1 with a,b,c, the half axes of the shape
ellepsoid. Rotations may have to be includud, if the shape does not
have a symmetry axis parallel to any low-index reflection. The K value
1.15 for the spherical domains would apply here.
For more anisotropic domains rod-like : J1 * sinc, H >> R (for instance carbon nanotubes and other fibers)
disk-like:
J1 * sinc, R >> H (for instance clay platelets) In these
cases the K factor for rods (0.9) applies for meridional reflections
along the axes (rods) of perpendicular to the basal plane (platelets),
while in the equatorial direction the disk factor K=1.05 should be
applied.
As special but common case in soft materials are
lamellae and hexagonal cylinders, for instance in block copolymers or
surfactant mesophases. The linear K=0.9 value should be applied for the
lamellar reflections, while the disk K=1.05 value would apply for the
hexagonal reflections.
The derivation given here
simplifies Patterson's original treatment making use of the modern
language of Fourier transforms, but reproduces his result for a
spherical domain of K=1.15. A more or less spherical shape may be the
most commonly encountered domain shape. Hence we would like to make a
point that, unless there is strong reason to believe that the domain
shape is strongly non-spherical, Patterson's K value of 1.15 should be
applied. In special situations where the scattering object can be
considered essentially 1D or 2D use of the other factors can be made.
C. C. Murdock, Phys. Rev. 35, 8 (1930)
B. E. Warren, Zeitschr. f. Krist. 99, 448
(1938)
A. L. Patterson, "The Diffraction of X-Rays by Small Crystalline
Particles", Phys. Rev. 56, 972 - 977 (1939)
A. L. Patterson, "The Scherrer Formula for X-Ray Particle Size
Determination", Phys. Rev. 56, 978 - 982 (1939)
B. E. Warren, "X-ray diffraction", Dover
