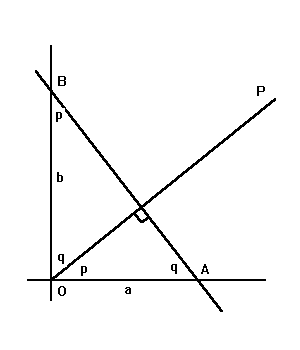Miller Indices
Steven Dutch, Natural and Applied Sciences, University of Wisconsin - Green
Bay
First-time Visitors: Please visit Site Map and Disclaimer. Use
"Back" to return here.
Lines in the Plane
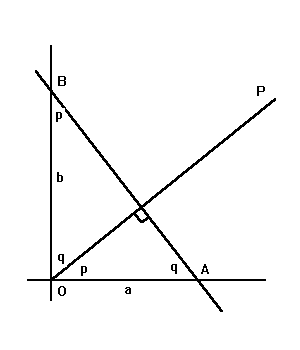 |
What are the equations of lines AB and OP?. The generic equation of a
line is y = mx + b, where b is the y-intercept and m is the slope. For
line AB, the slope is -tan q, or -b/a. Thus we have:
Line AB: y = -bx/a
+ b, or, x/a + y/b = 1.
If OP is perpendicular to AB, its y- intercept is obviously zero, and
we have y = x tan p, or y = xa/b, or xa = yb.
Thus, a general line has a simple equation in terms of its intercepts,
and a line through the origin perpendicular to the line also has a simple
equation in terms of the intercepts. As a general rule, if two lines are
perpendicular, the product of their slopes is -1. |
Lines and Planes in Three Dimensions
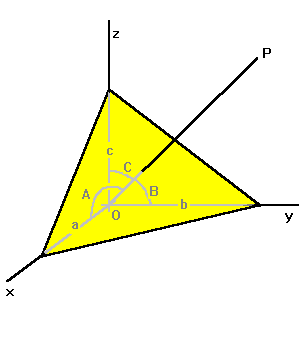 |
The equation for a plane in three dimensions is exactly analogous for
the line in two dimensions: x/a + y/b + z/c = 1.
If line OP is perpendicular to the plane, its equation is also
analogous to the two-dimensional case: xa = yb = zc.
If we know a plane, we know the line through the origin perpendicular
to it, called the pole to the plane. Quantities a, b and c are
termed the direction numbers of the line.
Line OP makes angles A, B, and C with the axes. The angles are related
as follows: cos2 A + cos2 B + cos2 C = 1
|
Cos A, cos B and cos C are called the direction cosines of the line.
They are obviously also direction numbers. If you know any arbitrary direction
numbers a, b and c, then cos A = a/s, cos B = b/s and cos c = c/s, where
s2 = a2 + b2 + c2
Miller Indices
Now that we know the equation of a plane in space, the rules for Miller
Indices are a little more intelligible. They are:
- Determine the intercepts of the face along the crystallographic axes,
in terms of unit cell dimensions.
- Take the reciprocals
- Clear fractions
- Reduce to lowest terms
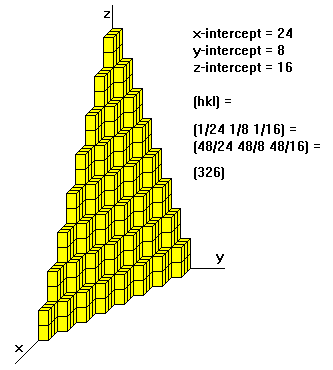
For example, if the x-, y-, and z- intercepts are 2,1, and 3, the Miller
indices are calculated as:
- Take reciprocals: 1/2, 1/1, 1/3
- Clear fractions (multiply by 6): 3, 6, 2
- Reduce to lowest terms (already there)
Thus, the Miller indices are 3,6,2. If a plane is parallel to an axis, its
intercept is at infinity and its Miller index is zero. A generic Miller index is
denoted by (hkl).
If a plane has negative intercept, the negative number is denoted by a bar
above the number. Never alter negative numbers. For example, do not
divide -1, -1, -1 by -1 to get 1,1,1. This implies symmetry that the crystal may
not have!
For hexagonal and trigonal minerals, there are three possible axis
directions, spaced 120 degrees apart:
+x2\ /-x3
\ /
\ /
\ /
\ /
-x1 \ / +x1
----------------+----------------
/ \
/ \
/ \
/ \
/ \
+x3/ \-x2
Obviously, any two intercepts specify the face. Also, there will be two
intercepts of one sign and one of the other. The Miller indices for a hexagonal
mineral are often written hikl. Indices h, i and k are related by h + i +
k = 0. Some modern texts dispense with the i term and treat hexagonal minerals
like all others.
Some General Principles
- If a Miller index is zero, the plane is parallel to that axis.
- The smaller a Miller index, the more nearly parallel the plane is to the
axis.
- The larger a Miller index, the more nearly perpendicular a plane is to
that axis.
- Multiplying or dividing a Miller index by a constant has no effect on the
orientation of the plane
- Miller indices are almost always small.
Why Miller Indices?
- Using reciprocals spares us the complication of infinite intercepts.
- Formulas involving Miller indices are very similar to related formulas
from analytical geometry.
- Specifying dimensions in unit cell terms means that the same label can be
applied to any face with a similar stacking pattern, regardless of the crystal
class of the crystal. Face 111 always steps the same way whether the crystal
is isometric or triclinic.
Miller Indices and Lines
The Miller Index of a line is about as simple as it can be: if the line
passes through (h, k, l), its Miller Index is [hkl], written in brackets to
distinguish it from a face.
Zones
A family of faces all parallel to some particular line is called a
zone, and the line is called the zone axis. Two faces (hkl) and
(pqr) belong to zone [kr-lq, lp-hr, hq-kp]. Note the similarity of this formula
to the cross-product formula from vector mechanics. Any other face (def) belongs
to the same zone if its indices are some linear combination of (hkl) and (pqr),
for example, d = 2h-3p, e = 2k-3q, etc.
For example, faces (110) and (010) belong to [1*0-0*1, 0*0-1*0, 1*1-1*0], or
[001]. The final zero in the face indices is a tipoff that they are both
parallel to the z-axis, and the zone index [001] is the z-axis. Any other
face whose index is some linear combination of (110) and (010) is also a member
of that zone. Obviously the final index must be zero.
What about faces (211) and (124)? Their zone axis is [1*4-1*2, 1*1-2*4,
2*2-1*1] or [2,-7,1]. Faces (335), (546), (1,-1,-3), etc. also belong to this
zone.
Return to Symmetry
Index
Return to Crustal
Materials (Mineralogy-Petrology) Index
Return to Professor Dutch's
Home Page
Created 9 Oct 1997, Last Update 14 Oct 1997
Not an official UW Green Bay site