Steven Dutch, Natural and Applied Sciences, University of Wisconsin - Green
Bay
First-time Visitors: Please visit Site Map and Disclaimer. Use
"Back" to return here.
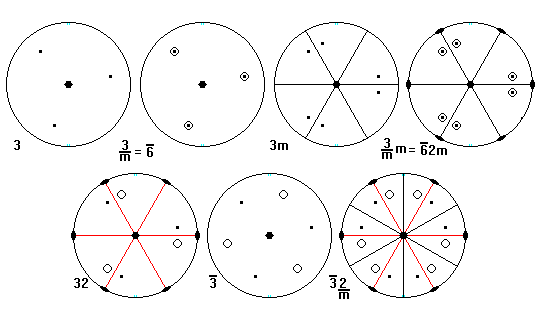
For more information on the 32 crystallographic point groups, see Crystallographic Point Groups.
Consider a system of symmetry axes with m and n-fold symmetry:
*A
180/n /|\ 180/n
/ | \
180/m / | \ 180/m
B*---+---*B'
180/m \ |O / 180/m
\ | /
180/n \|/ 180/n
*A'
Axis A rotates axis B to B' through an angle of 360/n. Likewise, axis B rotates A to A' through 360/m. Angle O is 90 degrees. In three dimensions, there are three possibilities:
Consider each case in turn
There are only two cases: n=4 and m=4, which gives rise to all the fourfold symmetries, and n=3, m=6, giving rise to all the three- and six-fold symmetries. There are also two- and one-fold patterns in the plane, which have to be considered in a different way because pairs of axes don't lead to closed patterns like that above.
Patterns on a sphere eventually must close, so we don't need to treat one- and two-fold symmetries differently. The possibilities are:
When m=6 and n = 3, 1/m + 1/n = 1/2 and we have the plane situation. When n has any value, we have the polar symmetries, with a major n-fold axis, possibly combined with mirror planes or two-fold axes. The other cases result in multiple 3-fold axes, the so-called isometric symmetries. The cases m=3 and m=4 result in crystallographic symmetries, the case m=5 results in the icosahedral symmetries.
On a negatively-curved (hyperbolic) surface, angles of a triangle sum to less than 180 degrees. Any values of m or n greater than those listed above will work. Unfortunately, we can't create more than a tiny portion of such a surface in three-space so we can't display these patterns without distortion. However, there are some distorted plane patterns and networks of polyhedra that display some aspects of this geometry. See approaches to hyperbolic patterns
The symmetries possible with a single three-fold symmetry axis illustrate the types of polar symmetry

There are seven types of symmetry. Recall that there are also seven one-dimensional strip space groups. The number seven is no coincidence: the polar symmetries can be obtained by wrapping the strip symmetries around a cylinder. The diagrams below show the strip, the result when wrapped around a cylinder, and a solid with the resulting symmetry.
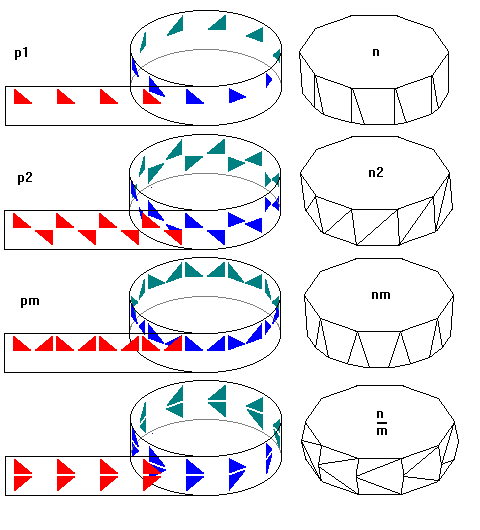
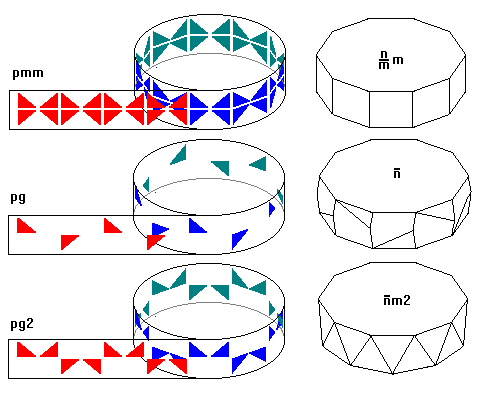
Regular prisms (regular polygon top and bottom faces and square prism faces) have nm/m symmetry. Regular antiprisms (regular polygons joined by a belt of equilateral triangles, have n'2m symmetry, where the prime denotes rotoinversion.
Perhaps the hardest symmetry to envision is rotoinversion symmetry, symbolized by a bar over the rotation number.
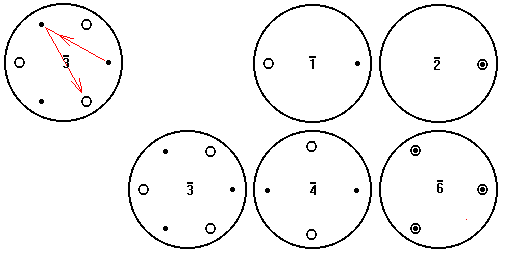
Rotoinversion requires rotating a point by 360/n degrees, then inverting it through the center as shown in the upper left. The crystallographic rotoinversion symmetries appear hopelessly random. However, when we consider non-crystallographic symmetries as well, the pattern leaps out.
The observation that the polar symmetries can be derived by wrapping the strip symmetries around a cylinder can help us understand rotoinversion symmetry from a different angle. Imagine the strips are transparent. If the period of the strip is not a rational fraction of the circumference of the cylinder the motif will repeat an infinite number of times. Otherwise, the pattern will eventually repeat and the cylinder will have overlapping motifs. For most symmetries this does not change the final result, but for glide symmetry (corresponding to rotoinversion), three cases are possible. Here we use "motif" to mean the pattern that results after the strip begins to repeat.
1. The motif coincides with itself
p b p p b p b p b p b
p b p p b p b p b p b
2. The motif is offset by one-quarter period after each revolution
p b p p b p b p b p b
p b p p b p b p b p
p b p p b p b p b p b
Final Result
p b p b p b p b p b p b p b p b p b p b p b p b p b p b p b p b
3. The motif is offset by one-half period after each revolution
p b p p b p b p b p b
b p b p p b p b p b p
Case 1 corresponds to the case where n is even and divisible by 4. Case 2 corresponds to n odd (there are more repetitions, more closely spaced). And case 3 corresponds to n even but not divisible by 4.
The relation of glide symmetry to rotoinversion was noticed a long time ago. Older crystallography texts sometimes called rotoinversion rotational reflection.
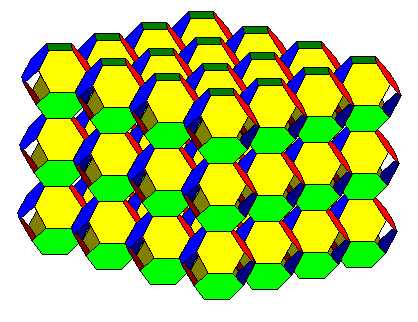 |
The pattern here is a "uniform polyhedron" in having all vertices alike and all faces regular. Here four hexagons meet at every vertex, something not possible on a plane or sphere unless the faces intersect themselves. This sort of pattern, sometimes termed a pseudopolyhedron, has some aspects of hyperbolic geometry. Unfortunately, it is not possible to model all hyperbolic symmetries this way. |
We get away with this only because the network of hexagons curls back on itself in our three-dimensional space. But on a "real" hyperbolic plane, we would see four hexagons meeting at every vertex and the surface would not curl back on itself. We can't make a physical model, we can only imagine it mathematically.
Return to Symmetry
Index
Return to Crustal
Materials (Mineralogy-Petrology) Index
Go to Recreational
Mathematics Index
Return to Professor Dutch's Home Page
Created 9 Oct 1997, Last Update 29 May 2003
Not an official UW Green Bay site