2009.09.25 - nonlin_bpm Studies

Revisit the use of nonlin_bpm to introduce gain and resolution errors. Recall the current procedure for introducing these errors:

• Start with 'beam' position at (x0,y0) = (1mm,1mm). Use nonlin_bpm to find button signals
• Move the 'beam' to (x0+dx,y0+dy), where (dx,dy) represent the resolution sigma. (Nominally dx,dy are the same). Use nonlin_bpm to find the new bi's.
• Use the average delta(bi) as the resolution in terms of button signals
• The final button signal with errors is therefore: bi' = gi*bi + delta(bi)*(rand), where (rand) = random Gaussian number

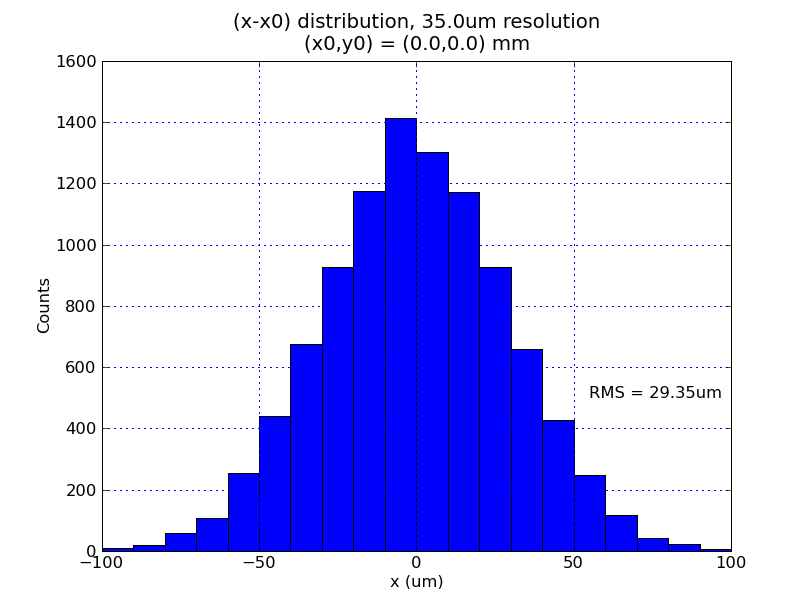
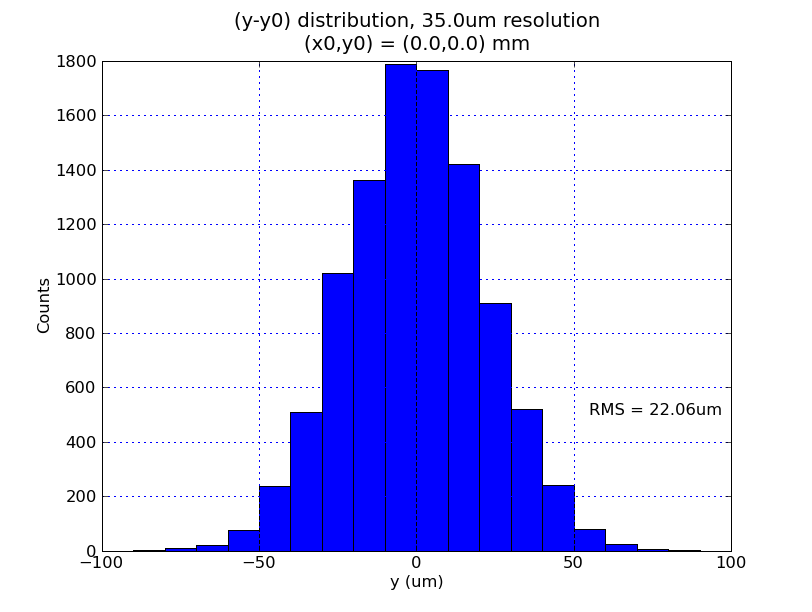
Using this method, examine the resulting distribution for 10,000 seeds when a 35um resolution is applied, without gain errors. First look at an "actual" position of (0,0):

The RMS of the distributions are a bit smaller than what we might want. Interestingly, the distribution is not symmetric in x and y. Strong dependence on the beampipe's asyemmetry? Try relocating the "actual" beam position to (1mm,1mm) and repeat:

Again, the distributions are both smaller than 35um and asymmetric between x and y.

What happens when we introduce gain errors, with no resolution? Apply random gain errors at the 1% level, and run for 10,000 seeds. Start at (x0,y0)=(0,0):

These plots seem very worrisome at first glance, however keep in mind that for each BPM the gain errors are fixed, not random on every measurement. This only results in a constant offset for each BPM with distribution RMS (132um,98um). With this in mind, consider the BPM/quad offset calibrations found by SBP. From detcal.ok, RMS offsets across all BPMs are (1.56mm,1.36mm). If these were solely due to BPM gain errors, what distribution of gains would account for this?

A gain error distribution of 12.5% seems to be close to what we'd expect if the observed offsets were actually gain errors.