Summary: Start with XR20m lattice and add errors at the following levels:
Note: these values come from the most recent survey data. Generate errors in ring_ma and simulate correction using a 2-stage technique:
Horizontal steerings aren't necessary, because the horizontal orbit is not perturbed significantly using these misalignment parameters. Apply these errors at 1/10, 1/2, and full values.
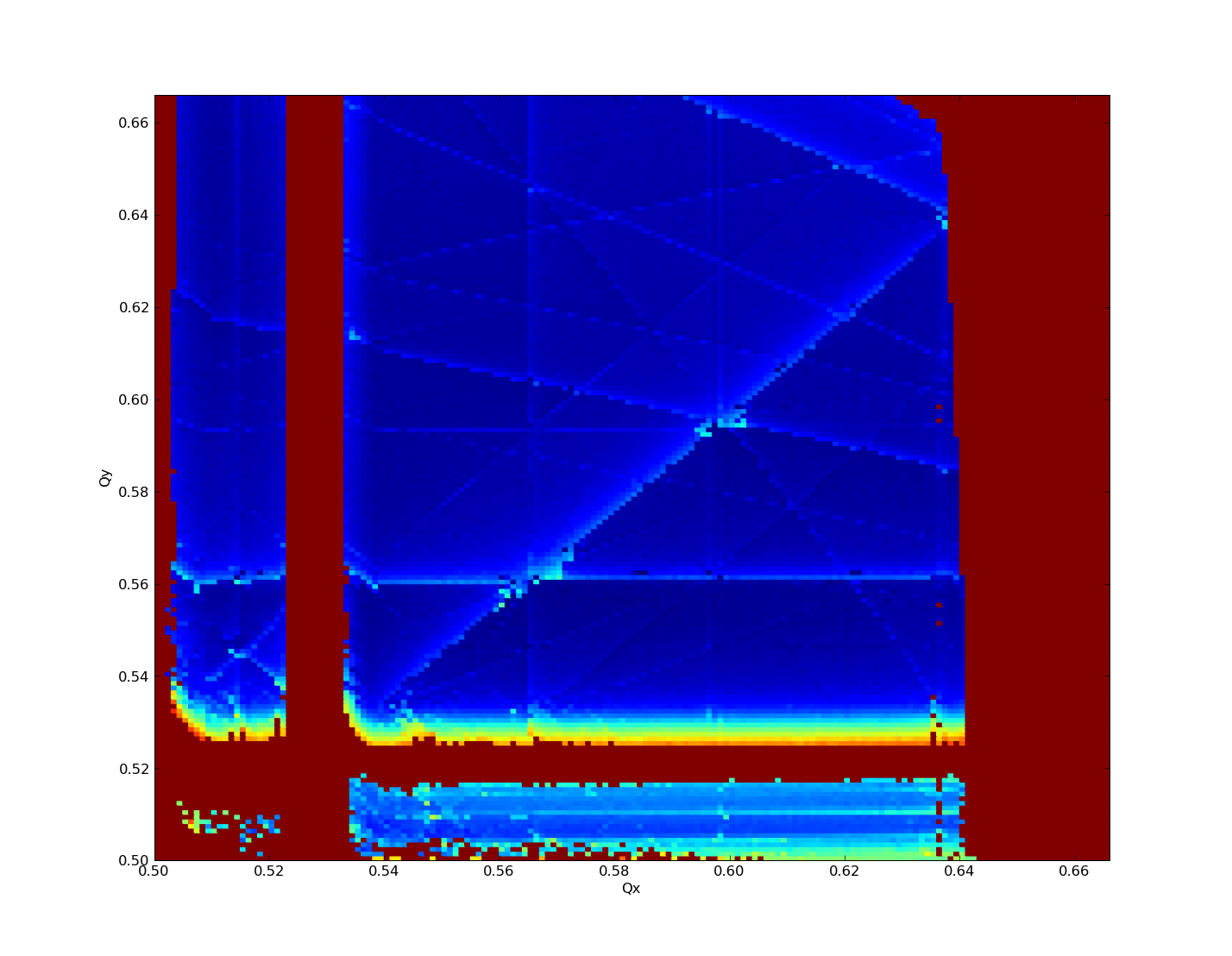
Run a tune scan on each resulting lattice from 0.5-0.666 in 0.002 steps. Plot the resulting data using a Python plotting script to ensure all scales are equivalent.
If we are to believe these results, this lattice is extremely sensitive to errors. There seems to be no fundamental difference between 10% and 100% errors, so far as the tune scan is concerned.
It also seems the 2Qx+Qz, 2Qx, and 2/3 Qx resonances disappear immediately when errors are applied. I am skeptical about this result. The primary resonances remaining are mQx + nQy + pQz, with m,n != 0.