The primary goal of the HelixIntersection facility is to calculate the intersection points of a KTHelix with a given list of surfaces, while performing user-specified operations on the KTHelix at each surface encountered. Because these operations are, in general, non-abelian, HelixIntersection needs to perform ray tracing to determine not only which surfaces are intersected, but also the order in which they are intersected. This problem is trivial to solve for concentric cylinders (as in the DR), but for partially overlapping surfaces (as in the SVD), the procedure is more involved.
Originally, HelixIntersection was designed to provide an interface between the track fitters, which implement a Kalman filter technique, and the geometry and material description of the CLEO detector (encapsulated in the DetectorGeometry package). However, the design of HelixIntersection has been generalized to support other applications, such as segment finding in the silicon detector.
Any track fitting algorithm needs the derivatives of the distance of closest approach (DCA) of a track to a given hit with respect to the five (or more) track parameters. It is possible to implement these derivative calculations approximately uniformly for all types of surfaces, but in general, these derivatives depend on the geometry of the sense surface where the hit occurs.
Also, the Kalman filter modifies the error matrix of a track based on the expected energy loss and multiple scattering at each measurement point along the trajectory. Therefore it is necessary for the track propagator to accumulate a description of the material traversed.
A final requirement is to decouple the intersection surfaces from the detector's geometry description. In the CLEO II implementation of the Kalman filter, it was found that proper behavior could not be achieved unless stops were taken within a single silicon wafer. Otherwise, the multiple scattering induced by an entire wafer would lie outside the Gaussian regime. Therefore, it should be possible to create intersection surfaces that lie between real physical boundaries of the detector elements.
The HelixIntersection package consists of two main components:
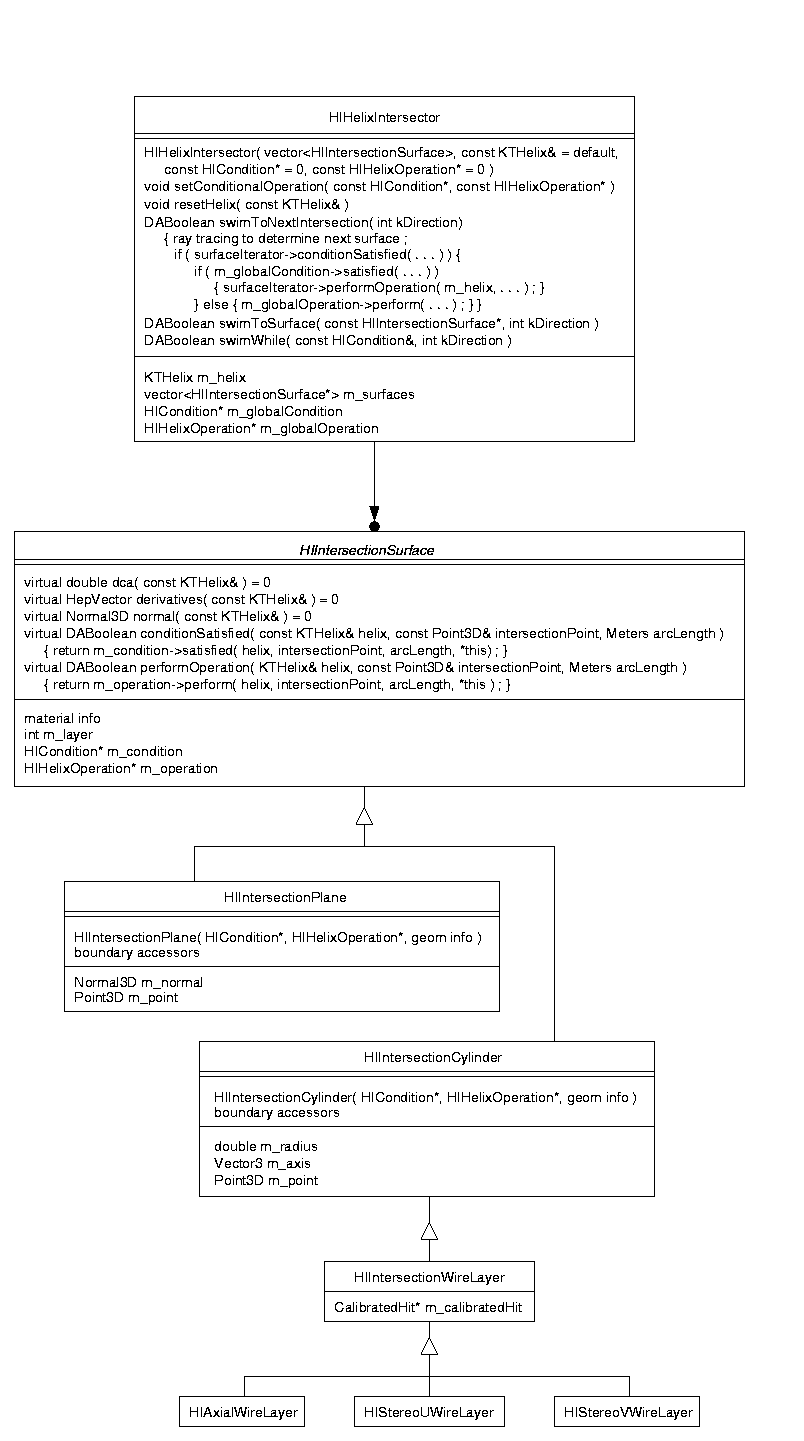
The intersection surfaces are generated by the user by parsing the DetectorGeometry. These surfaces can take any arbitrary shape, but will most commonly be planes or cylinders. The use of planes and cylinders provides easy interaction with KTHelix, which contains member functions moveToPlane(...) and moveToCylinder(...). The surface is a boundary between two physical volumes, and, therefore, it has access to the material properties of both these volumes. Each surface also contains member functions for calculating the DCA and its derivatives, given a KTHelix.
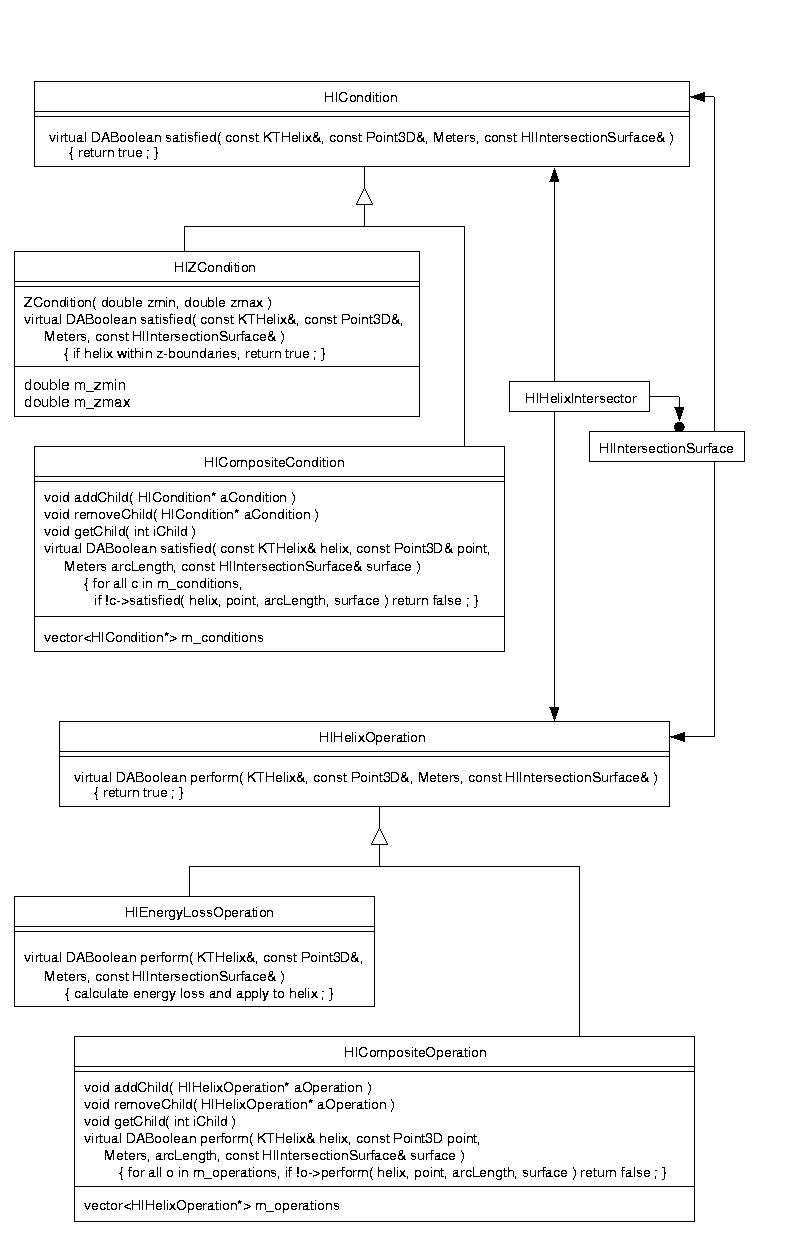
In determining whether a helix intersects a given surface, one may want to enforce additional conditions. For instance, one basic condition is that the track's position should lie within the physical z-boundaries of the detector element. These conditions are given by the user and are encapsulated in a separate object, to which the surfaces holds a pointer.
Once an intersection has been established and the helix has been propagated to that point, the user may wish to modify the helix. In the case of the Kalman filter, the energy of the track needs to be updated to reflect its passage through material and the width of the Gaussian multiple scattering needs to be calculated. The specific operation to be performed may vary with the type of surface. Therefore, as with the conditions described above, each surface also contains a pointer to an object that encapsulates these operations.
Both the condition classes and the operation classes are implemented as Composites. In other words, objects that contain a single condition (or operation) have the same interface as objects that contain multiple conditions (or operations) because both inherit from the same base class. However, instead of implementing a specific condition, the composite condition contains a list of other concrete conditions, each of which is executed in turn. Thus, whether the object is a single condition or a container of other conditions is transparent to the user.
The helix intersector encapsulates the interactions between the KTHelix and the intersection surfaces. To find the surfaces intersected by the helix, the intersector performs ray-tracing operations and then checks whether the condition associated with each surface is met. Then, the intersector propagates the helix appropriately. At each surface encountered, the intersector performs the associated helix operation.
Just as with the intersection surfaces, the helix intersector also contains pointers to a condition object and an operation object. However, this condition is applied globally, after each intersection has been found. Before performing the operation associated with the surface intersected, the helix intersector tests this global condition. If satisfied, it overrides the surface's operation with the global operation. Otherwise, the surface's operation is executed. A typical use of the global condition and operation might be to check the number of radiation lengths to the next intersection. If it exceeds some nominal value, then the global operation would propagate the helix to some intermediate distance instead of performing the surface's operation.
The class diagrams below show only the most salient features of each class, omitting trivial constructors, accessors, and member data.
To use the HelixIntersector package, the user first creates an STL vector of HIIntersectionSurface objects, which also entails creating the HICondition and HIOperation objects associated with each HIIntersectionSurface. Then, the HIHelixIntersector is initialized with the vector of HIIntersectionSurfaces and the KTHelix under consideration. The user also calls the member functions of the HIHelixIntersector to propagate the KTHelix from surface to surface. A brief description of each class is given below.