


Next: ESTIMATIONS OF NEUTRINO TOROID
Up: nanp97
Previous: nanp97
It is well known that the electromagnetic properties of a particle
with spin 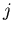 are described by
are described by 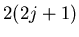 form factors.
Thus, for spin-
form factors.
Thus, for spin-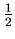 particles different parametrizations of
electromagnetic current contain four independent form factors.
Using the multipole
parametrization we may find its nonrelativistic counterparts and call
them the charge, magnetic, toroid and electrical dipole form factors.
After Ya. Zel'dovich introduced the anapole for the Dirac particle
in 1957 [1], it is
generally believed that a geometrical model of the anapole is poloidal
currents on a torus. Indeed, a model like this corresponds to
the toroid dipole form factor, rather than the anapole as the latter
coincides with the toroid form factor only for the current diagonal on
initial and final masses [2]. This circumstance is especially
important in the framework of neutrino physics in connection with the
problems of neutrino decay, oscillation processes and so on.
A large number of articles are devoted to the problem of appearance
of the anapole or the toroid
dipole in the elementary particle theory. Nonetheless, up to date these
characteristics are the most mysterious and ambiguous. For example,
we may remark that the anapole cannot radiate while the toroid dipole can,
because the former is a composition of two multipole parameters, the
time derivative of the electric dipole moment and the toroid dipole moment,
working in opposite phases so that their radiation amplitudes cancel
each other.
In our context it is important to cite the articles by V. Ginzburg and
V. Tsytovich [3], who calculated the intensities of
the Vavilov-Cherenkov and
transition radiation of the toroid dipole moment within the
classical approach, and by A. Gongora-T. and R. Stuart [4],
who demonstrated the gauge invariance of the
field-theoretical calculation of the anapole in the framework of
the Standard Model.
Based on this knowledge and Ref. [5],
we continue the search for the possibilities of fixing the toroid
moment contributions along the lines outlined in Refs. [6]
and [7]. Our withdrawal from the common approach is caused by the
fact that we
take into account both massive and masless neutrinos
and limits of low and high
energies. Recall the permitted forms of couplings for the
electromagnetic current
particles different parametrizations of
electromagnetic current contain four independent form factors.
Using the multipole
parametrization we may find its nonrelativistic counterparts and call
them the charge, magnetic, toroid and electrical dipole form factors.
After Ya. Zel'dovich introduced the anapole for the Dirac particle
in 1957 [1], it is
generally believed that a geometrical model of the anapole is poloidal
currents on a torus. Indeed, a model like this corresponds to
the toroid dipole form factor, rather than the anapole as the latter
coincides with the toroid form factor only for the current diagonal on
initial and final masses [2]. This circumstance is especially
important in the framework of neutrino physics in connection with the
problems of neutrino decay, oscillation processes and so on.
A large number of articles are devoted to the problem of appearance
of the anapole or the toroid
dipole in the elementary particle theory. Nonetheless, up to date these
characteristics are the most mysterious and ambiguous. For example,
we may remark that the anapole cannot radiate while the toroid dipole can,
because the former is a composition of two multipole parameters, the
time derivative of the electric dipole moment and the toroid dipole moment,
working in opposite phases so that their radiation amplitudes cancel
each other.
In our context it is important to cite the articles by V. Ginzburg and
V. Tsytovich [3], who calculated the intensities of
the Vavilov-Cherenkov and
transition radiation of the toroid dipole moment within the
classical approach, and by A. Gongora-T. and R. Stuart [4],
who demonstrated the gauge invariance of the
field-theoretical calculation of the anapole in the framework of
the Standard Model.
Based on this knowledge and Ref. [5],
we continue the search for the possibilities of fixing the toroid
moment contributions along the lines outlined in Refs. [6]
and [7]. Our withdrawal from the common approach is caused by the
fact that we
take into account both massive and masless neutrinos
and limits of low and high
energies. Recall the permitted forms of couplings for the
electromagnetic current
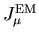 :
:
where the matrix elements are taken between the Dirac or Majorana neutrino
states with different masses in general.
A Lorentz-covariant structure of the dressed vertex operator
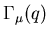 is given by:
is given by:
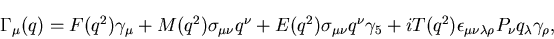 |
(2) |
where 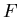 ,
, 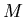 ,
, 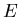 and
and 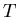 are the normal, anomalous magnetic,
electric and toroid dipole form factors respectively,
are the normal, anomalous magnetic,
electric and toroid dipole form factors respectively,
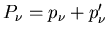 and
and
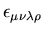 is the antisymmetric tensor.
It is easy to check that for the Majorana current only the
toroid dipole form factor survives [8]. Moreover, if the current
considered is diagonal on the initial and final masses, the anapole and
toroid parametrizations coincide. Then the interaction of the Majorana
neutrino with the electromagnetic field is described by
is the antisymmetric tensor.
It is easy to check that for the Majorana current only the
toroid dipole form factor survives [8]. Moreover, if the current
considered is diagonal on the initial and final masses, the anapole and
toroid parametrizations coincide. Then the interaction of the Majorana
neutrino with the electromagnetic field is described by
In the nonrelativistic limit
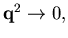 where
where
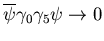 and
and
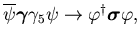 we find:
we find:
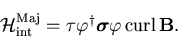 |
(4) |
In the static limit (
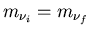 ) for Dirac neutrinos
we may utilize the following nonrelativistic approximation for the interaction
energy:
) for Dirac neutrinos
we may utilize the following nonrelativistic approximation for the interaction
energy:
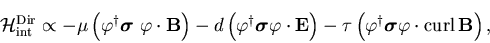 |
(5) |
where 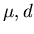 and
and 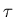 are the magnetic, electric and toroid dipole moments
respectively.
The magnetic and electric dipole moments are odd under
both the temporal and spatial reflections, and the toroid dipole
moment is T invariant and does not conserve P- and C-parities individually,
see Table 1.
are the magnetic, electric and toroid dipole moments
respectively.
The magnetic and electric dipole moments are odd under
both the temporal and spatial reflections, and the toroid dipole
moment is T invariant and does not conserve P- and C-parities individually,
see Table 1.
The complete analysis of the current properties with non-diagonal
masses are given [9].



Next: ESTIMATIONS OF NEUTRINO TOROID
Up: nanp97
Previous: nanp97
2001-08-02