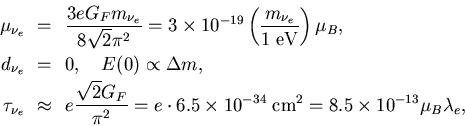ESTIMATIONS OF NEUTRINO TOROID DIPOLE MOMENT

We define the toroid dipole moment (TDM) of the neutrino as the strength of the contact interaction of axial-vector current with the external electron current or the local vortex magnetic field, or the time-dependent electric field, see (3, 4). In accordance with this definition, the toroid dipole moment and the form factor of the mass eigenstate of the Majorana neutrino in the one-loop approximation of the Standard Model were calculated in Ref. [5]. The calculations were performed by the dispersion method, all external particles were on the mass shells and there were no problems with the physical interpretation of the final result. The case of Majorana neutrinos was chosen as a common example of the calculation with the three-flavor basis and the $i=1, ..., k$ mass basis of Majorana neutrinos ( $\nu_{l} = \sum_{i} K_{li} N_{i}$) with a rectangular $3 \times (3+k)$ mixing matrix. The TDM is determined by the matrix elements of the mixing matrices $K$, leptons, quarks and $W,Z$ bosons masses and has the absolute value of the order of $e\cdot\left(10^{-33} - 10^{-34}\right) \mbox{cm}^2.$ This value is very sensitive to uncertainties of quark masses which define the upper and lower limits of the TDM of the mass eigenstates of Majorana neutrinos. We also found that the TDM has a finite value in the case of massive and massless neutrinos. If there is no mixing in the lepton sector, i.e. $K = 1$, we can define the singular electromagnetic characteristics, the toroid moments, of the three weakly interacting massless neutrinos as:

$$\begin{eqnarray*} \tau_{\nu_e} &\approx& e\Bigl[+\,6.873\;\;{\rm to}\;+8.112\B... ...71\;\;{\rm to}\;-0.732\Bigr] \times 10^{-34} \quad {\rm cm}^2. \end{eqnarray*}$$

This result can be extended to Dirac neutrinos. Since the antiparticle contribution in the massless limit is equal to the particle contribution, the TDM of the Dirac neutrino is half of the Majorana one. Using the numerical calculations and results of Ref.  [5] we present the behavior of the toroid form factors of massless flavor neutrinos, $\nu_{e, \mu, \tau},$ for a wide range of $q^2\equiv t$: $0 \leq \vert t\vert / 2m^{2}_{W} \leq 10^{-2}$ in Fig. 1. This interval covers all possibilities of testing this quantity in the low-energy scattering experiments.

In order to discuss a different application of toroid interactions, induced by toroid dipole moments of neutrinos, we recall the theoretical values and experimental limits for three dipole moments  [5,6,10,11]:

• theoretical calculations:
  $$\begin{eqnarray*} \mu_{\nu_e}\!& = &\! \frac{3eG_F m_{\nu_e}}{8\sqrt{2}\pi^2}=... ...\times10^{-34}\;{\rm cm}^2 = 8.5\times10^{-13} \mu_B\lambda_e, \end{eqnarray*}$$
  
  
  
  
  
  where $\mu_B$ is the Bohr magneton and $\lambda_e$ is the electron Compton wavelength.
• experimental bounds:
  $$\begin{eqnarray*} \tau_{\nu_e}&\Rightarrow & {\rm unknown}, \nonumber \\ \mu... ...\vert\mu_{\nu_e}+id_{\nu_e}\vert &\leq& 1.5\times10^{-10}\mu_B. \end{eqnarray*}$$