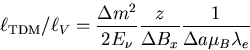The vacuum TDM may play a very important role for neutrino
oscillations. For instance, let us consider the evolution equation of three
Majorana neutrinos
![]() in the
presence of electromagnetic interactions induced by their toroid dipole
moment (further we will call this type of interactions as the toroid
ones)
in the
presence of electromagnetic interactions induced by their toroid dipole
moment (further we will call this type of interactions as the toroid
ones)
In this sense, this problem is an analog of the well-known
Wolfenstein equation for the propagation of neutrinos through a
medium [12], but the resonance conversion of neutrinos
can occur even in the vacuum due to the toroid interactions of neutrinos
(if
![]() ).
The off-diagonal matrix elements
).
The off-diagonal matrix elements ![]() ,
induced by the transition toroid moments, are nontrivial factors in
the Wolfenstein equation and had no previous analogs in the SM
(beyond the scope of SM this role was played by the so-called flavor
changing neutral currents). Since the Hamiltonian of the evolution of the
three neutrino flavors contains at least one time-dependent
external parameter
,
induced by the transition toroid moments, are nontrivial factors in
the Wolfenstein equation and had no previous analogs in the SM
(beyond the scope of SM this role was played by the so-called flavor
changing neutral currents). Since the Hamiltonian of the evolution of the
three neutrino flavors contains at least one time-dependent
external parameter
![]() ,
we should take into account the topological phases in the evolution
operator [13], which may be very important
for neutrino oscillations [14]. If, in addition, a neutrino
beam intersects some density fluctuations and element compositions
in the background of matter, a new phenomenon, geometric resonance,
occurs in neutrino oscillations [15]. The two
time-dependent parameters of the Hamiltonian (varying independently
of each other), which are needed for the geometric resonance, can be
the external electromagnetic field (in the medium, it can
be the electron current and/or intrinsic sources) and the medium
itself (
,
we should take into account the topological phases in the evolution
operator [13], which may be very important
for neutrino oscillations [14]. If, in addition, a neutrino
beam intersects some density fluctuations and element compositions
in the background of matter, a new phenomenon, geometric resonance,
occurs in neutrino oscillations [15]. The two
time-dependent parameters of the Hamiltonian (varying independently
of each other), which are needed for the geometric resonance, can be
the external electromagnetic field (in the medium, it can
be the electron current and/or intrinsic sources) and the medium
itself (
![]() ). For example, if
). For example, if
![]() and the particle number density
and the particle number density ![]() vary cyclically when the neutrino beam propagates through the medium,
i.e.,
vary cyclically when the neutrino beam propagates through the medium,
i.e.,
![]() and
and
![]() for some time
for some time ![]() , they form a closed contour on the plane
(
, they form a closed contour on the plane
(
![]() ,
, ![]() ), and
for some neutrino momentum the geometric resonance takes place
(for details, see [15]).
In order to estimate the contribution of toroid interactions to
the transition probability of neutrino conversion we simplify eq. (1)
to two neutrino scenario. Then the probability of the
), and
for some neutrino momentum the geometric resonance takes place
(for details, see [15]).
In order to estimate the contribution of toroid interactions to
the transition probability of neutrino conversion we simplify eq. (1)
to two neutrino scenario. Then the probability of the
![]() conversion can be represent as
conversion can be represent as
![\begin{displaymath}P(\nu_\alpha\rightarrow\nu_\beta) = \sin^22\theta\sin
\int_0...
...u
\mbox{\boldmath $\sigma$}\cdot
{\rm curl}{\bf B}\right]dt. \end{displaymath}](img82.png)