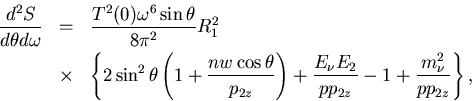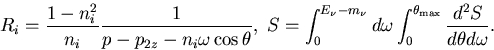Next: CONCLUSION
Up: APPLICATIONS OF TOROID INTERACTIONS
Previous: The estimation of interference
The neutrinos with the TDM as well as the neutrino with the magnetic moment
produce the transition radiation (TR) when crossing the interface between
two media, see Fig. 4, with the plasma frequencies
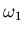 and
and 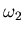
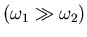 [7].
We calculate the probability of the TR of the (Majorana) neutrino TDM.
The (contact) electromagnetic interaction of the neutrino field
[7].
We calculate the probability of the TR of the (Majorana) neutrino TDM.
The (contact) electromagnetic interaction of the neutrino field
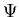 with the classical
external current is described by the Hamiltonian density:
with the classical
external current is described by the Hamiltonian density:
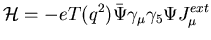 |
|
|
(1) |
It is shown in Ref. [7] that TR becomes possible if
there is a plane interface at 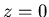 , where the refractive index
suddenly changes from
, where the refractive index
suddenly changes from 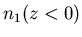 to
to 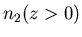 .
Using eq. (1) in the Born approximation, we can
express the transition matrix element as
.
Using eq. (1) in the Born approximation, we can
express the transition matrix element as
Here
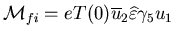 is the amplitude, and
is the amplitude, and 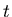 ,
, 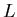 and
and 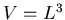 denoted the time, length and volume
respectively. Here
denoted the time, length and volume
respectively. Here
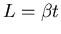 , where
, where 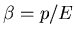 is the velocity of the neutrino.
In connection with the phase in the integrand of (2)
the formation zone length of the medium may be defined as
is the velocity of the neutrino.
In connection with the phase in the integrand of (2)
the formation zone length of the medium may be defined as
where 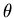 is the angle between the photon and the direction of the
incident neutrino. The details of further calculations are
the same as in [7] and we present here the final results
for the total energy of the transition radiation
is the angle between the photon and the direction of the
incident neutrino. The details of further calculations are
the same as in [7] and we present here the final results
for the total energy of the transition radiation
where
The total energy loss of the neutrino in the process of the medium -
vacuum
transition was computed numerically and its dependence on 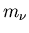 is given in Fig. 5.
is given in Fig. 5.
The fact that massive neutrinos with the magnetic moment can produce
TR is well known. It should be pointed out that the nonzero TDM of the neutrino
gives rise to the TR for massive and massless neutrinos.
This interesting fact requires a separate investigation.



Next: CONCLUSION
Up: APPLICATIONS OF TOROID INTERACTIONS
Previous: The estimation of interference
2001-08-02
![]() and
and ![]()
![]() [7].
We calculate the probability of the TR of the (Majorana) neutrino TDM.
The (contact) electromagnetic interaction of the neutrino field
[7].
We calculate the probability of the TR of the (Majorana) neutrino TDM.
The (contact) electromagnetic interaction of the neutrino field
![]() with the classical
external current is described by the Hamiltonian density:
with the classical
external current is described by the Hamiltonian density: