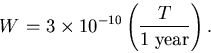![]() Let us consider a neutrino with non-zero toroid dipole moment
crossing the interface between two media, see Fig. 1,
with refraction indices
Let us consider a neutrino with non-zero toroid dipole moment
crossing the interface between two media, see Fig. 1,
with refraction indices ![]() and
and ![]() (
(![]() ).
The electromagnetic interactions
of neutrinos is described by the Hamiltonian:
).
The electromagnetic interactions
of neutrinos is described by the Hamiltonian:
Here ![]() ,
, ![]() ,
,
![]() ,
, ![]() and
and ![]() are the neutrino wave function, neutrino toroid
form factor, electromagnetic current,
are the neutrino wave function, neutrino toroid
form factor, electromagnetic current, ![]() potential and tensor of
the electromagnetic field, respectively
(the Hamiltonian (6) was also obtained by Zel'dovich
[10] using the anapole parametrization).
potential and tensor of
the electromagnetic field, respectively
(the Hamiltonian (6) was also obtained by Zel'dovich
[10] using the anapole parametrization).
The transition
![]() becomes
possible due to the TDM of the neutrino
becomes
possible due to the TDM of the neutrino ![]() .
In a medium with refraction index
.
In a medium with refraction index ![]() ,
the four-momentum vector of a photon is given by
,
the four-momentum vector of a photon is given by
![]() (
(![]() is the
energy of a photon), and the transition probability reads
is the
energy of a photon), and the transition probability reads
![]() , where
the transition matrix element is expressed as
, where
the transition matrix element is expressed as
Using the numerical value (1),
![]() with
with
![]() , and assuming
that the refractive index can be expressed as
, and assuming
that the refractive index can be expressed as
![]() for
for
![]() (
(![]() is the plasma frequency) for a medium-vacuum
transition (
is the plasma frequency) for a medium-vacuum
transition (![]() ,
, ![]() ), we present the energy spectrum
and angular distribution in Figs. 2 and 3.
The total energy loss of the neutrino has been computed numerically
and is shown as a function of the neutrino mass for
), we present the energy spectrum
and angular distribution in Figs. 2 and 3.
The total energy loss of the neutrino has been computed numerically
and is shown as a function of the neutrino mass for ![]() MeV
in Fig. 4. For
MeV
in Fig. 4. For ![]() eV
the TR energy is approximately constant and equals
eV
the TR energy is approximately constant and equals
![]() keV. Because of the finite value of the TDM
for massless neutrinos [4,5], the TR does not
vanish in this limit and has the value
keV. Because of the finite value of the TDM
for massless neutrinos [4,5], the TR does not
vanish in this limit and has the value
![]() keV.
keV.
In order to estimate the magnitude of this effect, let us consider
a transition radiation detector (TRD) which can be used
to measure experimentally such transition radiation of neutrinos.
The TRD consists of sets (![]() ) of ``radiator'' and xenon-gas
chambers, where one radiator typically comprises of a few hundred
layers (
) of ``radiator'' and xenon-gas
chambers, where one radiator typically comprises of a few hundred
layers (![]() ) of a polypropylene film (
) of a polypropylene film (![]() eV) and a
gas (
eV) and a
gas (![]() eV). The total energy deposition (
eV). The total energy deposition (![]() ) in the TRD
is given by
) in the TRD
is given by