J. Knobloch
Motivation for cavity research
The need for particle accelerators
In the early days of this century, three "elementary" particles had been identified -- the electron, the proton, and the neutron. All matter known at the time could be explained in terms of these constituents. However, the simple picture offered by these particles was already shattered within a few decades. By the 1960's a myriad of new "elementary" particles were discovered that threatened to be very confusing. Being driven by a desire to find an underlying simplicity, researchers expended much effort to explain the multitude of particles in terms of even more fundamental "building blocks." This endeavor culminated in the development of the "Standard Model." According to this model, there are a total of 24 fundamental particles: six "flavors" of quarks arranged in three generations of two, six leptons (also in three generations) and an equal number of antiparticles. By combining quarks of different flavors, all mesons and baryons known to date can be explained.
Parallel to the development of the elementary particle picture, the large number of different forces observed in nature was not understood. But, beginning with the unification of the electric and magnetic forces, all forces were eventually shown to be different manifestations of four fundamental ones -- the electromagnetic force, the weak force, the strong force and, gravity. These forces are transmitted by bosonic particles, of which 13 are believed to exist. Salam, Weinberg, and Glashow in the 1970's then developed the theoretical framework for the unification of the electromagnetic and the weak forces by a single
electroweak force. Only below energies of 1 TeV does it manifest itself as two seemingly separate forces. Three fundamental forces remain. However, it is postulated that these three are also unified at much higher energies. (The strong and electroweak forces at >= 10
12GeV and gravity at >= 10
19GeV.)
Past and current particle accelerators have proved pivotal in providing the experimental evidence that vindicates the Standard Model, which now is accepted as one of this century's great successes. For example, in 1983 researchers at CERN proved the existence of the W
+, W
-, and Z
0particles, three of the four carriers of the electroweak force (the photon is the fourth carrier). And only as recently as 1995 was the postulated sixth quark (the "top") discovered at Fermilab, to complete the three generations of quarks.
Nevertheless, mysteries remain. Why do quarks have mass? Why are they so much heavier than leptons? Why is there a preponderance of matter over antimatter in the universe? Why are there three generations of quarks and leptons, when only the first generation is sufficient to describe the tangible universe? (For an in depth discussion of many outstanding questions, see Reference
[1] .) Answers to some of these and other questions, it is hoped, will be provided by future generations of particle accelerators.
Frontier accelerators
Accelerator research is rapidly progressing on two main frontiers: Pushing the beam energy and increasing the beam current/luminosity. For example, in the last 12 years the beam energy has increased by a factor of 10.
Currently, the highest energy accelerators are the p-pbar Fermilab Tevatron (1 TeV in the center of mass) and the LEP e
+e
-accelerator at CERN (165 GeV in the center of mass). The two are roughly complementary. (Because protons and antiprotons are each made of three quarks, the collision energy is shared among the six constituents involved. According to conventional wisdom, a p-pbar accelerator has to be roughly six to ten times as energetic as an e
+e
-accelerator to probe the same physics.) The luminosity record, on the other hand, is currently held by the Cornell Electron Storage Ring (CESR) at 3 x 10
32cm
-2s
-1, operating at a modest 10.6 GeV in the center of mass (CM).
To be able to probe new physics, the next generation of accelerators has to be an order of magnitude higher in energy and about two orders of magnitude higher in luminosity.
The energy frontier has to be extended to 1 TeV (for e
+e
-accelerators) or more to be able to search for the Higgs particle which, it is hoped, will distinguish between a number of different theories of electroweak symmetry breaking. The theories attempt to explain matters such as the mass of quarks and the dramatically different behavior of the weak and electromagnetic forces. Because the (non-resonant) cross-section of interesting events reduces quadratically with increasing energy, the luminosity also has to be increased with the square of the beam energy.
Two machines proposed to push the energy frontier are the Large Hadron collider at CERN (pp, 14 TeV CM) and the TeV superconducting linear collider TESLA at DESY (e
+e
-, 1 TeV CM). ( Linear colliders based on normal conducting cavities have also been proposed (e.g., the NLC).) Both require luminosities of 1 -- 2 x 10
34cm
-2s
-1.
The current/luminosity frontier is also being advanced at lower energies to enable researchers to observe rare events such as the decay of B and Bbar mesons. These decays are believed to violate charge-parity (CP) symmetry, which may explain why matter is much more abundant in the universe than antimatter. However, CP violation is an extremely rare event, and over 10
7B-Bbar pairs need to be produced annually for effective studies. Luminosities in excess of 10
34cm
-2s
-1are needed.
High current, high luminosity storage rings to produce copious numbers of B-Bbar's ("B-factories") for CP violation studies are planned (and now being constructed) at KEK in Japan and at SLAC. These accelerators are not pushing the energy frontier, but rather are increasing the stored current to new levels. One to two amperes will be stored in the KEK B-factory to reach a luminosity 3 x 10
33cm
-2s
-1. (The KEK B-factory will be operating with asymmetric beam energies so that lower luminosities than 10
34cm
-2s
-1are sufficient.)
Omitted in this discussion entirely, but equally important, are new accelerator facilities designed not for particle physics but for other applied research. They include light sources (e.g., SOLEIL in France), tritium production for defense and potential fusion applications (e.g., the ATP at Los Alamos), neutron sources for materials research (e.g., the ANS) and the accelerator based transmutation of nuclear waste products (ATW). In many cases they also push accelerator technology to new levels.
[2]
Superconducting cavities
It is the devices used to provide energy to the particles that are crucial to an accelerator. Most commonly used are radio frequency (rf) cavities, an example of which is shown on the right.
In the past, copper cavities were used for acceleration (e.g., at SLAC). However, superconducting technology has proven itself over the last ten years as a promising alternative, being used in machines such as HERA (Hamburg, Germany) and TJNAF (Newport News, VA). Continuous wave (cw) accelerating gradients of 10 MV/m have been achieved, exceeding levels that are possible with copper cavities. Many of the future projects (among them TESLA, LEP-II, the KEK B-factory, and the LHC) are relying on superconducting cavities to achieve their design goals. Thus, superconductors will play a pioneering role at both the energy frontier and the high current frontier. In some very imaginative and novel designs (for example multi-TeV muon colliders), superconducting rf is completely indispensable, illustrating that this technology holds the key for the next generation of particle accelerators and perhaps even beyond. Extensive research has therefore been performed to understand the performance limitations of superconducting cavities and to improve upon the achieved accelerating gradients. The work described here is similarly motivated.
Advantages of superconducting cavities
Although not completely loss free above T = 0 K, as in the dc case, superconducting cavities dissipate orders of magnitude less power than normal conducting cavities. Niobium cavities, like those installed at TJNAF, routinely achieve quality factors 100,000 to 1,000,000 times that of copper cavities. The dramatically reduced resistivity translates into a number of very important advantages. They include:
[2]
- Operating cost savings. Even when taking into account the cost of refrigerating superconducting cavities, their power demand in cw applications is more than two orders of magnitude less than that of equivalent copper cavities.
- Capital cost savings. The reduced power requirements translate into capital cost savings, since fewer (and sometimes simpler) klystrons are needed.
- High gradient. The reduced power consumption also enables superconducting cavities to operate at high cw gradients.
- Reduced impedance. The aperture of superconducting cavities is large, thereby minimizing disruptive interactions of the cavity with the beam (characterized by the impedance). Higher currents can therefore be accelerated. (Cavities are the main source of impedance in an accelerator.) This fact is the main motivation for using superconducting rf technology in high current machines such as CESR.
Cavity performance limitations
A limit on the maximum accelerating gradient of superconducting cavities is imposed by the rf critical magnetic field. At no point of the cavity surface may the magnetic field exceed the rf critical field, otherwise the superconductor goes normal conducting ("quenches"). Niobium cavities of the shape used in our test are therefore limited to an accelerating gradient of about 50 MV/m.
For a number of reasons, though, such high accelerating gradients are never achieved in practical cavities. The most common limiting mechanisms are
field emission, thermal breakdown, and, at times,
multipacting .
[2]
Field emission is the primary mechanism that limits present day cavities to accelerating gradients below 25 MV/m. In the presence of a high surface electric field, rf power is lost to electrons that tunnel out of the cavity wall at very localized points. The emitted electrons are accelerated by the electromagnetic fields and, upon impact, heat the cavity wall and produce x-rays. Field emission scales exponentially with the electric field and is capable of consuming inordinate amounts of power.
Thermal breakdown generally results when a highly resistive defect on the rf surface causes a large fraction of the cavity to quench. An abrupt reduction of the cavity quality results. Thermal breakdown can also be initiated by the heat from bombarding field emission electrons.
Multipacting is a resonant process, in which a large number of electrons build up an avalanche by repeated impact with the cavity walls. Again, the heat deposited by these impacts can lead to thermal breakdown. In the absence of thermal breakdown, the absorption of rf power by multipacting electrons can still make it impossible to raise the cavity fields.
Even at low field levels (below an accelerating gradient of a few MV/m) all cavities display losses higher than theoretically e xpected. The anomalous losses are attributed to a temperature independent
residual resistance . The dominant sources for this resistance are impurities on the rf surface, adsorbed gases, and residual magnetic flux that is trapped in the superconductor as it is cooled through the transition temperature. (Mu-metal is used to shield cavities from the earth's magnetic field, but residual fields always remain in the cryostat.) In some cases the precipitation of niobium hydride at the rf surface due to hydrogen stored in the wall may also contribute to the residual resistance. This phenomenon is known as the "Q-virus", and it can be avoided by driving out the hydrogen during a vacuum bake of the cavity at 900 C.
Studying loss mechanisms
As we have seen, the key to increasing accelerator performance needed for future applications lies with our ability to improve the rf cavities. Even current proposals such as TESLA are pushing state of the art superconducting technology to the limit. It is therefore imperative, both out of fundamental interest and for the important forthcoming applications, that we gain a better understanding of the anomalous losses in cavities.
Experimental approach
Thermometry
One extremely successful scheme in the study of cavity losses has been thermometry. Its strength lies in the fact that ultimately each loss mechanism produces heat in the cavity wall. Thermometry thus can be used for the study of
all types of losses.
The generic setup consists of an array of thermometers placed on the exterior surface of the cavity (left). The thermometers typically are carbon resistors specially prepared to insulate them from the cryogen (helium), yet allowing them to be in thermal contact with the cavity surface. Below 4.2 K the exponential increase of the thermometers' resistance with decreasing temperature allows for sensitive measurements at the millikelvin level.
The effectiveness of temperature mapping was first demonstrated by Lyneis in 1972.
[3] Since then, thermometry has been used as a powerful diagnostic tool by numerous laboratories.
[4-13] Its strengths has been proven repeatedly. For example, it has been possible to locate thermal breakdown sites and field emitters. It is these and other successes that gave the impetus for the construction of a new system used for the studies at Cornell.
This newly developed system (for 1.5 GHz cavities) improves significantly on previous designs in two important categories: speed and sensitivity. The fastest system to date for comparable cavities required about 15 s for the acquisition of a temperature map.
[4,14] The resolution of this system was limited to temperature signals above 5 mK, so that many low level losses went undetected. A high sensitivity system, using a lock-in amplifier, was developed as well, which could resolve microkelvin temperature signals.
[5,6] However, map acquisition times up to 50 minutes were needed and transient effects (such as the activation and deactivation of field emitters) could not be studied.
In contrast, our new system is able to acquire temperature maps in less than 0.2 s while still resolving signals at the 150 microkelvin level. Both of these features have been critical in our study of low level losses and transient behavior. An increased resolution of 30 microkelvin is even possible if the acquisition time is lengthened to 2.5 s.
Microscopy
Past studies with 3 GHz cavities have shown that thermometry data can be used successfully to locate anomalous losses (especially field emission), whose source may subsequently be studied in an electron microscope.
[15,16]
With this success in mind, we developed a system to cleanly dissect cavities following their rf tests (left), for further analysis in an electron microscope and an energy dispersive x-ray system (above). The latter is used for the elemental analysis of defects.
Our improved thermometry system, combined with a second setup to measure the cavity quality, and our ability to examine the rf surface in a microscope provided us with a very powerful set of tools to study loss mechanisms. A measurement of the cavity quality sums the power dissipation of all active loss mechanisms. For detailed studies we then use thermometry to localize the sources of these losses. Due to the system's improved resolution, new losses, that previously have gone undetected, can now be observed. Temporal changes in power dissipation, that often provide vital information on the mechanisms involved, can now also be recorded because of the higher speed of the thermometry system. Finally, the microscopy enables us to correlate the temperature data with the physical properties of lossy sites -- an important step that was lacking in many previous cavity studies.
Experimental objectives
Armed with this new setup, we set out to systematically study both low and high field losses. In particular, we hoped to find active emission sites, since these dominate the behavior of present day cavities.
To learn to control the impact of emission, we need to fill in the gaps in our understanding of emitter behavior. What are the questions that beg to be answered?
A quantum mechanical analysis of field emission (the Fowler-Nordheim theory) predicts that the current should
not be significant below 1 GV/m.
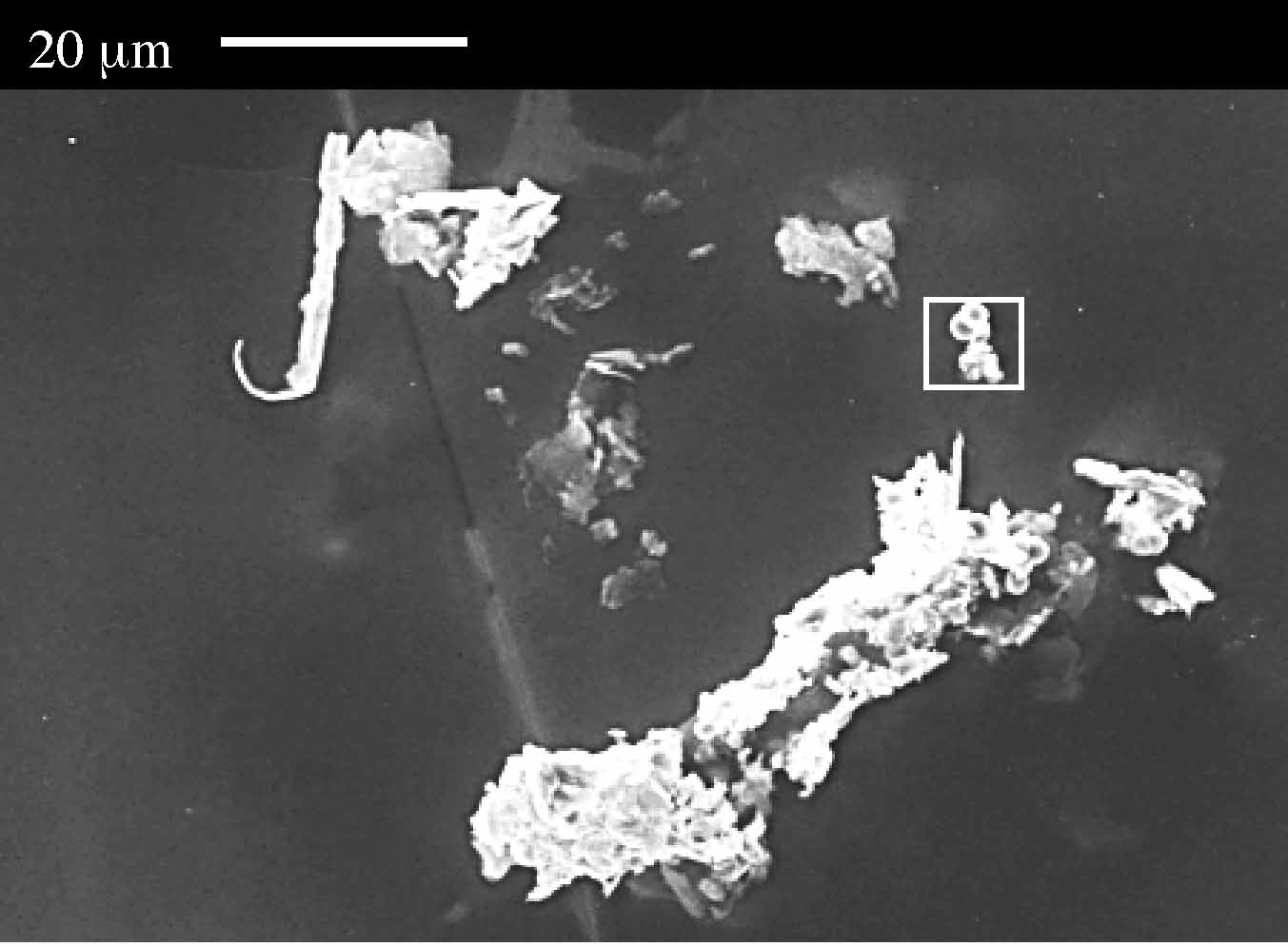
[17] But then, why is field emission so prevalent in rf cavities? In previous dc field emission studies, micron size metallic particles with jagged features were found to be a prolific source of emitters (right). Is the same true of field emission in rf cavities? Until this study, active emitters in rf cavities had never been located and examined with surface analytic instruments. Our experiments demonstrate that indeed metal particles, sometimes jagged, are often found to cause emission in cavities (right). This (often qualitative) observation fits with the traditional view, that the geometric enhancement of the electric field facilitates field emission. However, it is hard pressed to account for field enhancement of more than 10 -- 100, as is frequently observed. We also found, on occasion, that smooth particles and even flat sites can emit. A more sophisticated model is therefore required to explain the enhanced emission.
Field emission in both dc studies and rf cavities is frequently found to be unstable. When the electric field is increased for the first time, emission will switch on, and it continues even if the electric field is lowered to values where no emission was previously recorded. We observed such events frequently during our studies. But what is the cause of activation? We have shown that on some occasions the arrival of particles is a simple cause. There have been several studies that suggest condensation of gas can also activate emitters.
[18,19] Does this take place at particle sites as well? Our results confirm gas activation in many cases. In particular, we identified a particulate emitter that showed reproducible increases in emission with experimental conditions that promoted the condensation of gases on the particles. Decreases of emission consistent with gas removal were also observed.
Occasionally emitters also switch off abruptly, this being known as
processing or
conditioning. Here more is already known. DC high voltage studies with niobium and copper electrodes have shown that field emission is almost always a pre-cursor to voltage breakdown, and that the breakdown event destroys the emitter (e.g.,
[20-22]) The breakdown event is associated with a discharge and its accompanying plasma. Frequently multiple (micron size) craters are found at the site of the discharge.
Yet, there are outstanding issues about emitter processing by discharge. Is the mechanism in rf cavities the same as that for dc gaps? What is the chain of events that take place between emission and voltage breakdown? What are the factors that govern the conditions for the formation of the discharge? For example, where does the gas for the discharge come from? Does the gas play any role in the field emission process before breakdown? Certain emitters will process at a given field, while others will not. What determines whether an emitter is processable? The experimental part of our work was designed to address many of these questions.
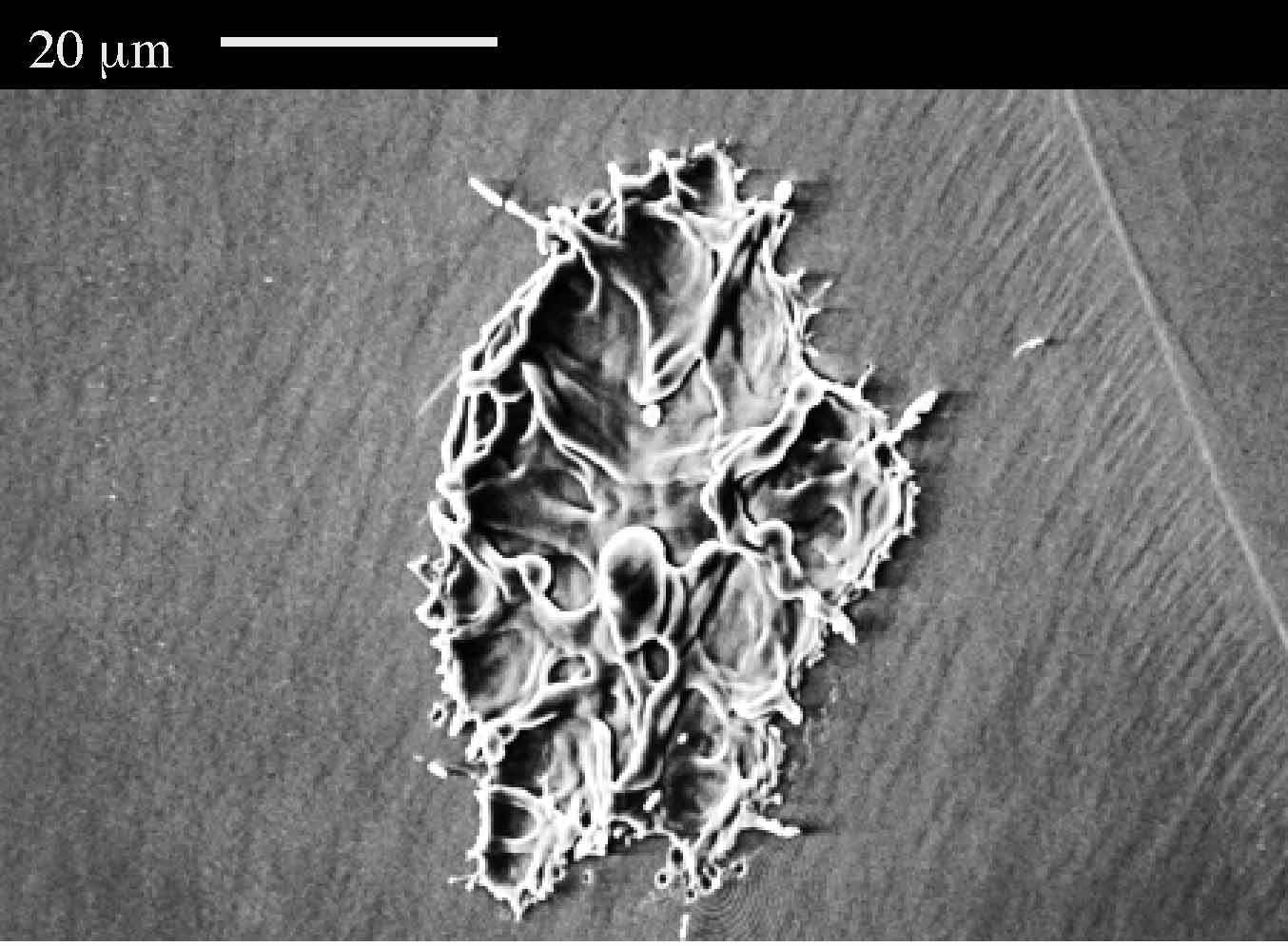
Prior to these experiments, we assumed that the heating by the field emission current alone is responsible for initiating the explosion. Our experiments, though, proved this hypothesis to be wrong. Microscopy revealed new features of emission sites that help us to draw a more complete picture of how field emission progresses to discharge. The evidence suggests that a plasma can coexist with rf emission before the onset of the discharge, and that gases play an important role in the progression of an emitter from steady state emission to its explosion. At first, parts of the emitter (microtips) melt due to Joule heating from the emission current. The vapor that evolves from the melting tip provides the initial source of gas that ultimately is responsible for initiating discharge.
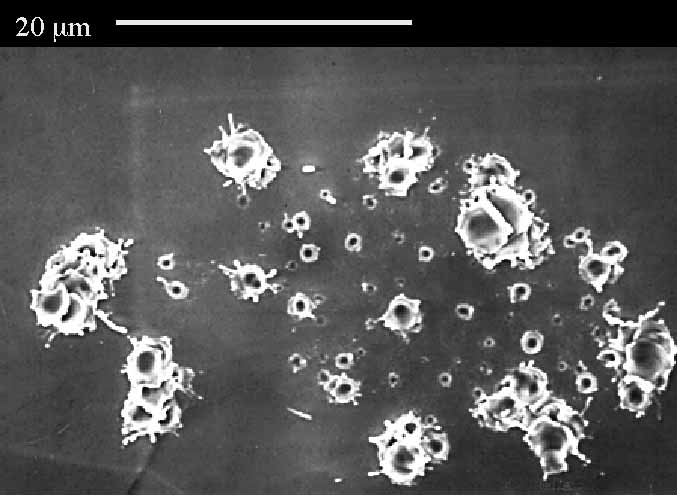
What is puzzling about the geometric field enhancement model of emission is the observation that large areas of the rf surface, many tens of microns across, can melt during the processing of an emitter (see, for example, above), even though steady state emission is from sub-micron regions. In many instances suchregions are also surrounded by small "satellite" craters (right). How does field emission continue after the microtip of the emitter melts? What produces the satellite craters? Again, we found that the plasma present during the discharge can explain such features.
When the field level and the accompanying emission current is not sufficient to initiate a discharge spontaneously, it is possible to deactivate emitters by the intentional addition of helium gas in the superconducting cavity (known as
helium processing ). How does helium processing work? A number of helium processing mechanisms have been identified. We were able to demonstrate, for the first time, that one important mechanism involves discharge. This discovery also emphasizes the important role played by gas during the transition from steady state field emission to discharge.
Guided by such experimental findings, we developed numerical simulations to model the electron impact ionization of gases evolving from hot emitters. The simulations reveal some of the mechanisms underlying the discharge. Newly created ions bombard the emitter and can lead to further gas evolution. Once a sufficiently dense gas builds up and large numbers of ions accumulate near the emitter, considerable electric field enhancement results that leads to an instability in the emission current. A discharge is then created.
The improved understanding can account for certain characteristic features of discharge events, such as the occurrence of satellite craters at emission sites. The simulations also provide the basis for an understanding of the conditions required for processing. For example, both the current density and total current drawn from an emission site need to exceed threshold values. Furthermore, our simulations set a time scale for the formation of discharge conditions.
We also intended to use the advanced thermometry to gain insights into other important aspects of superconducting cavity behavior. We were able to advance our understanding of thermal breakdown, multipacting, and residual surface resistance mechanisms. We have identified an interaction between thermal breakdown and the activation of field emission via the gases released during the breakdown. The advanced thermometry system also enabled us to recognize weak and short lived multipacting, and we found interesting examples of the activation of field emission by gases released during multipacting. Gas discharge events initiated by multipacting were documented as well, and we showed that the discharge can reduce the residual surface resistance. We also identified new sources of residual losses, due to foreign particles as well as magnetic flux generated and trapped during thermal breakdown or multipacting events.
#References
References
- R. Peccei et al. Particle Physics: Perspectives and Opportunities . World Scientific, Singapore, 1995. Report of the DPF Committe on Long-Term Planning.
- H. Padamsee, J. Knobloch, and T. Hays. RF Superconductivity for Accelerators . Wiley and Sons, New York, 1998.
- C. M. Lyneis, M. McAshen, and N. T. Viet. In Proceedings of the 1972 Proton Linear Accelerator Conference , p. 98, Los Alamos, NM, 1972.
- H. Padamsee et al. Proceedings of the 1987 IEEE Particle Accelerator Conference , pp. 1824-1826, Washington D.C., 1987.
- P. Kneisel, G. Müller, and C. Reece. IEEE Transactions on Magnetics 23 (2), 1417-1421 (1987).
- C. E. Reece, Proceedings of the 3rd Workshop on RF Superconductivity , pp. 545-563, Argonne, Illinois, 1988.
- H. Piel, CERN Accelerator School: Superconductivity in Particle Accelerators , pp. 149-196, Hamburg Germany, 1988.
- P. Bernard et al. Proceedings of the 11th International Conference on High-Energy Accelerators , pp. 878-885, Geneva, Switzerland, 1980.
- B. Dwersteg et al. Proceedings of the 2nd Workshop on RF Superconductivity , pp. 63-73, CERN, Geneva, Switzerland, 1984.
- Q. S. Shu et al. Proceedings of the 1995 Particle Accelerator Conference , pp. 1639-1641, Dallas, TX, 1995.
- M. Pekeler et al. Proceedings of the 7th Workshop on RF Superconductivity , Gif-sur-Yvette, France, 1995.
- G. Müller et al. Proceedings of the 1st European Particle Accelerator Conference , p. 1289, Rome Italy, 1988.
- E. Kako et al. Proceedings of the 8th Workshop on RF Superconductivity , p 918-943, Newport News, VA, 1993.
- Field emission studies: An owner's manual . Technical report, Cornell University, Laboratory of Nuclear Studies, 1991. SRF/D report 910121-24, edited by W. Hartung.
- J. Graber et al. Nuclear Instruments and Methods in Physics Research A350 , 582-594 (1994).
- J. H. Graber. High Power Processing Studies of 3 GHz Niobium Superconducting Accelerator Cavities . PhD thesis, Cornell University, 1993.
- R. H. Fowler and L. Nordheim. Proceedings of the Royal Society London A119 , 173-181 (1928).
- Q. S. Shu et al. IEEE Transactions on Magnetics 25 , 1868-1872 (1989).
- M. Luong et al. Proceedings of the 7th Workshop on RF Superconductivity , pp. 509-511, Gif-sur-Yvette, France, 1995.
- G. A. Mesyats. IEEE Transactions on Electrical Insulation , 18 (3), 218-225 (1983).
- E. A. Litvinov, G. A. Mesyats, and D. I. Proskurovskii. Soviet Physics Uspekhi 26 (2), 138-159 (1983).
- B. Jüttner. Nuclear Instruments and Methods in Physics Research A268 , 390-396 (1988).
-